Laboratorio de computación científica WATSON
Spanish translation of an English article contributed by
Miss Eleanor Krawitz and published by Frank da Cruz, unveiling how in 1945 the Watson Scientific Computing Laboratory developed a scientific research center that used calculating machines.
 16 January, 2023 IBM Watson Laboratory today
16 January, 2023 IBM Watson Laboratory today
Original text published at http://www.columbia.edu/cu/computinghistory/krawitz/index.html.
Translated into Spanish by Juan for Ibidem Group
* * *
LABORATORIO DE COMPUTACIÓN CIENTÍFICA WATSON
Centro de Investigación Científica con Máquinas de Cálculo.
Un texto de Miss Eleanor Krawitz, Supervisora de Tabulación del Laboratorio de Computación Científica Watson
Columbia Engineering Quarterly, noviembre de 1949
En el transcurso de los últimos años se han logrado grandes avances en todos los campos de la investigación científica, y un factor importante en este avance ha sido el uso extensivo de métodos y equipos de computación automática. Hoy en día los cálculos se realizan de forma automática en laboratorios de todo el país. El desarrollo de estos laboratorios de computación es de particular interés para los estudiantes de Columbia ya que los primeros se establecieron aquí en la Universidad. La Oficina de Estadística de la Universidad de Columbia se estableció a finales de los años veinte para el uso de educadores y estadísticos. La Oficina Astronómica, creada en 1934, dirigida por el Dr. WJ Eckert y operada conjuntamente por la Universidad de Columbia, la Sociedad Astronómica Estadounidense y la Corporación Internacional de Máquinas Comerciales, funcionaba como una organización sin ánimo de lucro a la que podían acudir astrónomos de todo el mundo para realizar sus cálculos. En 1945, IBM creó un Departamento de Ciencias Puras, nombró al Dr. Eckert como su director y fundó el Laboratorio de Computación Científica Watson en el campus de la Universidad.
El objetivo principal del Laboratorio Watson es la investigación en las diversas ramas de la ciencia, especialmente las relacionadas con las matemáticas aplicadas y el cálculo numérico. Los servicios del laboratorio se ofrecen gratuitamente a cualquier científico o estudiante graduado que se dedique a una investigación que contribuya significativamente al progreso en los campos de la ciencia y que utilice máquinas calculadoras para lograr ese fin. Cada año, se otorgan dos becas del Laboratorio Watson en matemáticas aplicadas a estudiantes cuyo estudio o investigación involucra cálculos a gran escala. Los miembros del personal ofrecen cursos de instrucción en su campo de interés bajo los auspicios de diferentes departamentos de la Universidad. Los cursos para estudiantes graduados incluyen la operación y uso de las máquinas y métodos numéricos; El crédito académico por los cursos se puede obtener mediante la inscripción en la Universidad de la manera habitual. Se imparten clases especiales sobre el funcionamiento de las máquinas a intervalos regulares a profesionales, científicos visitantes de todo el mundo y estudiantes graduados que trabajan para obtener su doctorado. Una función adicional del Laboratorio Watson es la difusión de información técnica sobre métodos de máquinas matemáticas y tablas matemáticas; una biblioteca completa que cubre estos temas está disponible. Una función adicional del Laboratorio Watson es la difusión de información técnica sobre métodos de máquinas matemáticas y tablas matemáticas; una biblioteca completa que cubre estos temas está disponible. Una función adicional del Laboratorio Watson es la difusión de información técnica sobre métodos de máquinas matemáticas y tablas matemáticas; una biblioteca completa que cubre estos temas está disponible.
La investigación se ha completado con éxito en muchos campos de la ciencia en el laboratorio por miembros del personal y científicos visitantes. La siguiente es una lista parcial de proyectos completados o en progreso:
- Astronomía: integración de órbitas de planetas y asteroides,
- Geofísica: trazado de trayectorias de ondas de sonido bajo el agua para varias profundidades y direcciones,
- Óptica: cálculos que incorporan el método de trazado de rayos,
- Química: cálculo de energías de resonancia mecánica cuántica de compuestos aromáticos,
- Ingeniería: construcción de tablas de resortes y engranajes y cálculo de tensiones asociadas con cargas sísmicas,
- Economía: estimaciones de determinados coeficientes en las ecuaciones de modelos económicos, mediante multiplicación e inversión de matrices,
- Física: cálculos de probabilidades de transición de calcio,
- Cristalografía: evaluación de una Transformada de Fourier para la estructura de la insulina.
El laboratorio mantiene una amplia variedad de máquinas tanto de tipo digital como analógico; la máquina digital es la que esencialmente cuenta, mientras que la máquina analógica hace mediciones físicas. Estas calculadoras están diseñadas para resolver problemas de la manera más conveniente y para comparar diferentes métodos de solución para determinar el más eficiente.
La mayoría de las máquinas leen y escriben mediante el uso de la tarjeta perforada que proporciona un medio para manejar datos automáticamente. Por lo tanto, las tarjetas pueden procesarse a través de cualquier serie de calculadoras y tener cualquier secuencia deseada de operaciones realizadas en ellas. La principal ventaja de la técnica de la tarjeta perforada es que se puede realizar un gran número de operaciones similares en cantidad. Después de perforar los valores iniciales en las tarjetas, el procedimiento de la máquina es automático. La perforación puede tener lugar en cualquiera de las ochenta columnas de la tarjeta. Cada columna se subdivide en doce posiciones distintas, que representan los números enteros del 0 al 9, así como dos posiciones especiales de perforación denominadas X e Y. La perforación X se usa principalmente para designar una operación especial o un número negativo. Las letras del alfabeto se registran mediante dos punzones en una columna,
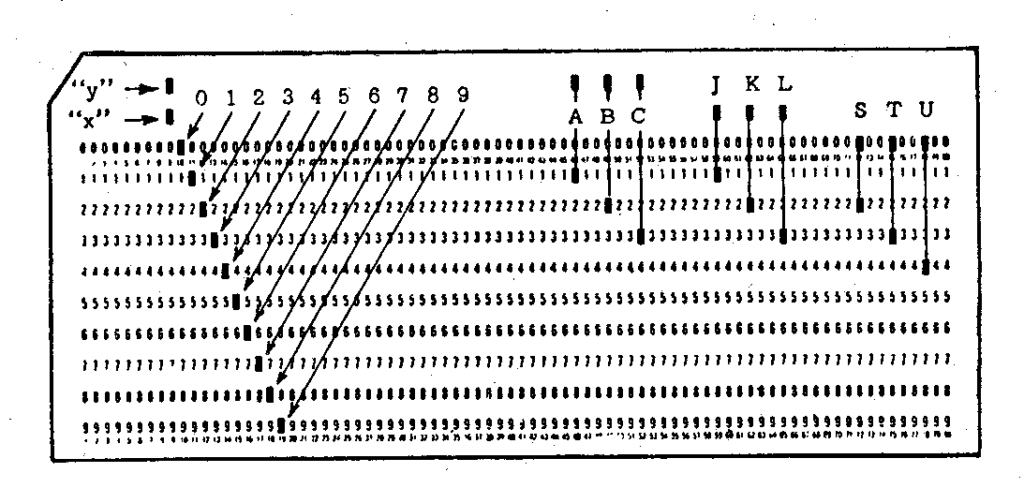
En todas las máquinas el principio de lectura de la tarjeta es el mismo. Los agujeros se perforan en las tarjetas y se leen por medio de contactos eléctricos hechos a través de los agujeros. La tarjeta, actuando como aislante, pasa entre un cepillo de alambre y un rodillo de latón (ver fig. 2).
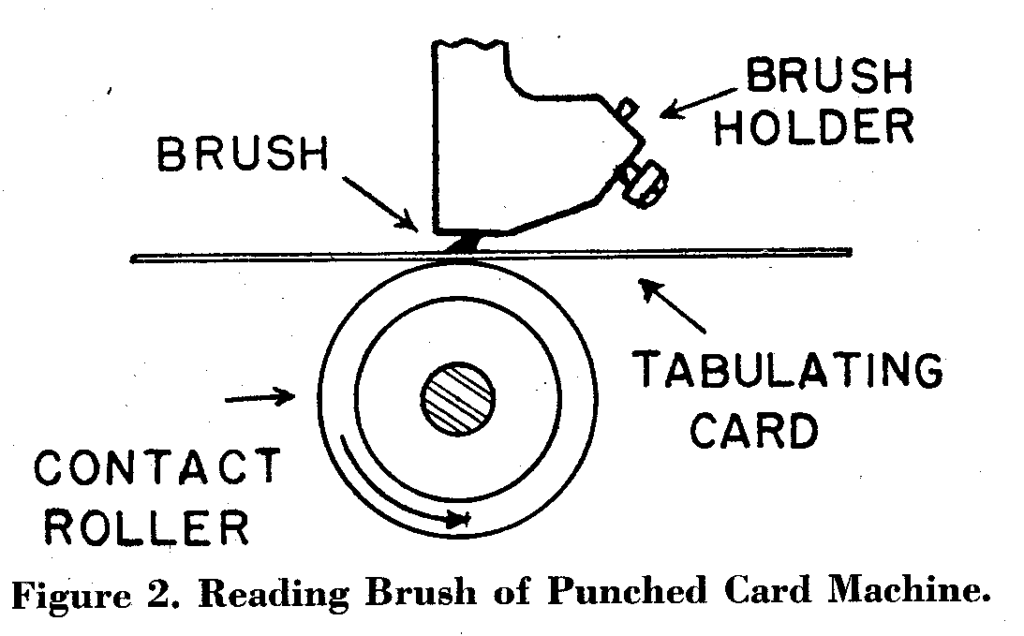
Un agujero perforado en la tarjeta permite que la brocha y el rodillo hagan contacto, completando así un circuito eléctrico; el impulso eléctrico está disponible en un panel de control enchufable, y la sincronización del impulso está determinada por la posición del orificio en la tarjeta. Todas las funciones de la máquina están gobernadas por la dirección de estos impulsos en el panel de control, y como resultado de la flexibilidad de este panel, se pueden realizar un gran número de operaciones. Un gran porcentaje de los problemas encontrados en el cálculo numérico se pueden manejar de manera eficiente en las máquinas estándar de IBM. El primer paso en el enfoque de estos problemas es traducir los datos originales al lenguaje de las calculadoras. Es decir, para grabarlo en forma de perforaciones en tarjetas estándar. Esta es la función del Key Punch. La información deseada se transcribe en la tarjeta presionando las teclas de la máquina en línea con la columna correspondiente. Estas tarjetas pueden introducirse en el Key Punch de forma manual o automática. A medida que se perfora cada columna, la tarjeta avanza automáticamente a la siguiente posición de perforación. Los punzones numéricos tienen catorce teclas; uno para cada una de las doce posiciones de perforación, una tecla de espacio y una tecla de expulsión de tarjeta. Los punzones alfabéticos cuentan, además, con un teclado de máquina de escribir que perfora automáticamente dos agujeros por columna. Habiendo sido codificadas por el Key Punch, las tarjetas están entonces listas para pasar por cualquiera de las otras máquinas requeridas para la solución del problema. Estas tarjetas pueden introducirse en el Key Punch de forma manual o automática. A medida que se perfora cada columna, la tarjeta avanza automáticamente a la siguiente posición de perforación. Los punzones numéricos tienen catorce teclas; uno para cada una de las doce posiciones de perforación, una tecla de espacio y una tecla de expulsión de tarjeta. Los punzones alfabéticos cuentan, además, con un teclado de máquina de escribir que perfora automáticamente dos agujeros por columna. Habiendo sido codificadas por el Key Punch, las tarjetas están entonces listas para pasar por cualquiera de las otras máquinas requeridas para la solución del problema. Estas tarjetas pueden introducirse en el Key Punch de forma manual o automática. A medida que se perfora cada columna, la tarjeta avanza automáticamente a la siguiente posición de perforación. Los punzones numéricos tienen catorce teclas; uno para cada una de las doce posiciones de perforación, una tecla de espacio y una tecla de expulsión de tarjeta. Los punzones alfabéticos cuentan, además, con un teclado de máquina de escribir que perfora automáticamente dos agujeros por columna. Habiendo sido codificadas por el Key Punch, las tarjetas están entonces listas para pasar por cualquiera de las otras máquinas requeridas para la solución del problema. un teclado de máquina de escribir que perfora automáticamente dos agujeros por columna. Habiendo sido codificadas por el Key Punch, las tarjetas están entonces listas para pasar por cualquiera de las otras máquinas requeridas para la solución del problema. un teclado de máquina de escribir que perfora automáticamente dos agujeros por columna. Habiendo sido codificadas por el Key Punch, las tarjetas están entonces listas para pasar por cualquiera de las otras máquinas requeridas para la solución del problema.

El clasificador se utiliza para organizar las tarjetas perforadas en cualquier orden numérico o alfabético que se desee, según la información que contengan. Las tarjetas a clasificar se alimentan desde una tolva a un solo cepillo, que lee la columna seleccionada y clasifica cada tarjeta en la adecuada de las trece casillas disponibles. Hay un bolsillo para cada una de las doce posiciones de perforación y uno para columnas en blanco. Mediante clasificaciones sucesivas, las tarjetas se disponen en cualquier orden deseado. La máquina, que funciona a una velocidad de 450 tarjetas por minuto, está equipada con un contador para registrar el número de tarjetas que pasan.
El intérprete alfabético está diseñado para traducir la información numérica o alfabética de la tarjeta en cifras impresas en cualquiera de las dos líneas en la parte superior de la tarjeta. Por lo tanto, la tarjeta perforada se lee más fácilmente y puede usarse como una tarjeta de archivo, así como en las máquinas.
La máquina de contabilidad es una máquina de sumar e imprimir de alta velocidad. Lee datos de una tarjeta, los suma y resta en contadores e imprime en una hoja de papel la información de las tarjetas o los totales de los contadores. La máquina enumera datos alfabéticos o numéricos a razón de ochenta tarjetas por minuto, o acumula hasta ochenta dígitos de totales a 150 tarjetas por minuto.
El perforador de reproducción transcribe todos o parte de los datos perforados en un juego de tarjetas a otro juego, o copia los datos de una tarjeta maestra a un grupo de tarjetas de detalles. El punzón tiene una unidad de comparación que compara los dos conjuntos de datos e indica cualquier desacuerdo entre los dos. La máquina se puede adaptar para su uso como una Perforación de Resumen para registrar en una nueva tarjeta los importes que se han acumulado en la Máquina de Contabilidad.
El Clasificador realiza algunas de las funciones del Clasificador de una manera más eficiente. Archiva dos juegos de tarjetas juntos, selecciona tarjetas particulares en cualquiera de los cuatro bolsillos de selección, empareja dos juegos de tarjetas de acuerdo con un número de control y verifica la secuencia de un juego de tarjetas. La máquina es muy flexible y permite el manejo de tarjetas según un patrón complicado que involucra la comparación de dos números de control. Las tarjetas pueden pasar por el Intercalador a razón de 240 a 480 por minuto.

El punzón de cálculo electrónico es una máquina de alta velocidad que utiliza circuitos electrónicos para realizar todas las operaciones básicas. Suma, resta, multiplica y divide los números introducidos en una tarjeta y marca las respuestas en la misma tarjeta o en una posterior. Realiza estas operaciones de forma repetitiva y en cualquier orden en una fracción de segundo. Calculating Punch lee los factores perforados en una tarjeta y realiza sumas, restas, multiplicaciones y divisiones, en el orden deseado. Se pueden perforar resultados separados para cada tipo de cálculo, o los resultados se pueden almacenar y usar como un factor para los siguientes cálculos. Esta máquina ha calculado diferencias de octavo orden de una función de once dígitos y muchas ecuaciones complicadas que implican un gran número de operaciones.
Además de las máquinas estándar descritas anteriormente, hay en el laboratorio una serie de calculadoras especialmente diseñadas que funcionan por medio de redes de relés y circuitos electrónicos. A continuación se muestra una breve descripción de estas máquinas especiales.
La Calculadora de retransmisión realiza todas las operaciones aritméticas básicas, incluida la determinación de raíces cuadradas a través de una red de retransmisión complicada. La extrema flexibilidad de esta calculadora se debe a su gran memoria interna, su rapidez en la realización de cómputos, su capacidad para leer simultáneamente cuatro tarjetas y perforar una quinta, y su capacidad para operar bajo un amplio y variado programa. La máquina está equipada con un circuito de clasificación para facilitar las operaciones de consulta de tablas. Se han resuelto muchos problemas complicados en una calculadora de relés, incluida la multiplicación de series armónicas, la multiplicación de matrices y ecuaciones diferenciales de sexto orden.
La calculadora de secuencia operada por tarjeta consta de una máquina de contabilidad que lee, suma, resta y almacena los datos, un punzón de resumen que perfora los valores finales, una caja de relés para brindar flexibilidad de control de las operaciones y una unidad que realiza multiplicaciones y divisiones. Las operaciones de las otras calculadoras generalmente se programan a través del cableado en el panel de control, mientras que esta máquina tiene esencialmente un panel de control básico configurado y se rige por perforaciones codificadas en la tarjeta. Esta calculadora ha demostrado ser particularmente hábil para calcular las órbitas de los asteroides.
El solucionador de ecuaciones lineales es un dispositivo eléctrico para la solución de ecuaciones lineales simultáneas hasta el duodécimo orden inclusive. Una vez establecidos los coeficientes de las ecuaciones en diales, interruptores o tarjetas perforadas, se ajustan las diferentes variables hasta obtener una solución. El método de solución es uno que da una convergencia muy rápida. Esta máquina fue construida en el laboratorio por el Sr. Robert M. Walker, miembro de nuestro personal, y el profesor Francis J. Murray del departamento de matemáticas de la Universidad.
La Máquina de Medición y Registro Controlada por Tarjeta está diseñada principalmente para la medición de fotografías astronómicas, aunque puede aplicarse fácilmente a fotografías en cualquier campo. Se introduce en la máquina una placa fotográfica de una porción del cielo que incluye la estrella en cuestión junto con una tarjeta perforada que indica las coordenadas aproximadas de la estrella. Luego, la máquina lee automáticamente la tarjeta perforada, ubica la estrella en la placa fotográfica a partir de estas coordenadas aproximadas, mide con precisión su posición y registra esta medida en una tarjeta. El registro de la tarjeta perforada queda entonces disponible para su tratamiento matemático.
Desde el inicio de la Oficina Astronómica en 1934, se han establecido varios laboratorios de tarjetas perforadas en la industria y el gobierno. Esos laboratorios en funcionamiento durante los años de la guerra desempeñaron un papel fundamental en nuestro programa de defensa nacional. En este grupo estaban los Laboratorios de Investigación Balística en Aberdeen, Maryland y Dahlgren, Virginia. En esta misma categoría estaba el Observatorio Naval de los Estados Unidos, que preparó tablas astronómicas para uso en navegación aérea y marítima, astronomía y topografía. En la industria, los laboratorios de computación han asumido un papel destacado en la investigación científica tanto pura como aplicada. Las técnicas de tarjetas perforadas se han empleado, por ejemplo, en la solución de problemas relacionados con el análisis de tensión y deformación de estructuras de aeronaves y el análisis de vibraciones de maquinaria grande.
Un ejemplo de la aplicación del equipo de tarjetas perforadas en problemas de la industria surge en el diseño y construcción de barcos, donde es necesario especificar las ubicaciones exactas de un gran número de puntos en la superficie. El diseñador puede lograr esto considerando varias secciones transversales a través del casco y representando el contorno de cada una de estas secciones mediante un polinomio de, digamos, quinto grado (ver fig. 3).
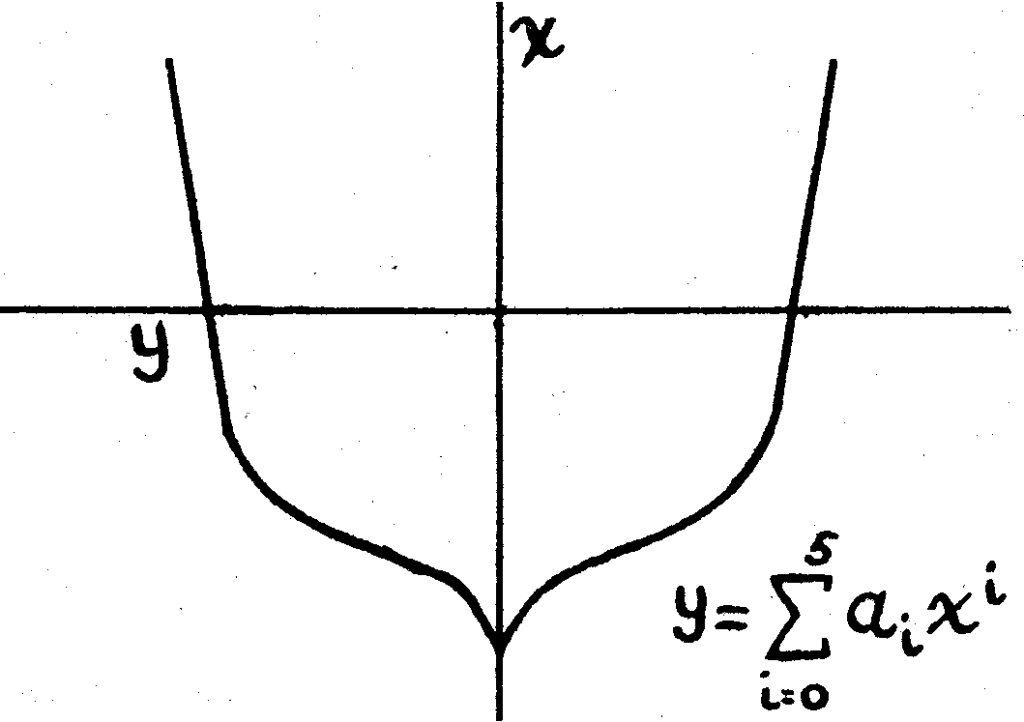
Figura 3. Sección transversal a través del recipiente
Los valores de las constantes, a 0 , …, a 5 , en la ecuación variarán con cada sección tomada, debido a la curvatura de la superficie en la dirección longitudinal. Por tanto, si el buque se divide en 200 secciones transversales, y es necesario determinar 100 puntos a cada lado del casco para cada sección transversal, habría que evaluar el polinomio 20.000 veces. El uso de equipos de tarjetas perforadas en la solución de este problema convierte un trabajo extremadamente engorroso en uno que la máquina calcula automáticamente después de completar la planificación original.

Supervisora de tabulación
Watson Scientific Computing Laboratory
La señorita Eleanor Krawitz, que tiene la distinción de ser la primera autora femenina en contribuir al COLUMBIA ENGINEERING QUARTERLY, puede presumir de muchos otros logros notables. Se graduó en 1943 de la escuela secundaria Samuel I. Tilden de Brooklyn, donde había sido miembro de la sociedad honoraria escolástica “Arista”. En Brooklyn College fue tesorera de Pi Mu Epsilon, sociedad honoraria de Matemáticas, hasta que recibió su licenciatura en Matemáticas en 1947. Luego trabajó como maestra suplente en Midwood High School y en su Alma Mater, Tilden High, pero pronto dejó de lado su carrera docente en la escuela secundaria para obtener su Maestría en Matemáticas en Columbia.
Actualmente, la señorita Krawitz es supervisora de tabulación en el laboratorio de computación IBM Thomas J. Watson de la Universidad de Columbia. No sólo está impartiendo clases de Astronomía en la Escuela de Graduados sobre el funcionamiento de las computadoras, sino que también se dedica a establecer procedimientos para el cálculo de problemas de física, matemáticas y astronomía.Eleanor Krawitz Kolchin falleció el viernes 25 de enero de 2019 a la edad de 92 años en Boca Raton, Florida. Estaba encantada con la atención que recibió a una edad avanzada debido a la publicación de este artículo en Internet en 2003 y su traducción a tantos idiomas. Sus últimas palabras para mí (en octubre de 2018) fueron “Casi todo no funciona aquí. Oooooo”.
Aportado por: Eleanor Krawitz Kolchin, noviembre de 2003. Escaneado
y convertido a HTML: sábado 22 de noviembre a las 17:06:54 de 2003
Convertido a HTML5: sábado 23 de febrero a las 08:52:56 de 2019
También por el autor:
- Krawitz, Eleanor, “Tablas matemáticas de tarjetas perforadas en equipos estándar de IBM”, Actas, Seminario de computación industrial , IBM, Nueva York (septiembre de 1950), págs. 52-56.
- Krawitz, Eleanor, “Matrix by Vector Multiplication on the IBM Type 602-A Calculating Punch”, Actas, Seminario de computación industrial , IBM, Nueva York (septiembre de 1950), págs. 66-70.
- Green, Louis C., Nancy E. Weber y Eleanor Krawitz, “El uso de energías calculadas y observadas en el cálculo de las fuerzas del oscilador y la regla de la suma f ” Astrophysical Journal , Vol.113 No.3 (mayo de 1951), págs. 690-696.
- Green, Louis C., Marjorie M. Mulder, Paul C. Milner, Margaret N. Lewis, John W. Woll, Jr., Eleanor K. Kolchin y David Mace, “Análisis de la función de onda de tres parámetros de Hylleraas para the He i Ground State in Terms of Central Field Wave Functions”, Physical Review 96, 319, 15 de octubre de 1954.
- Green, Louis C., Satoshi Matsushima, Cynthia Stephens, Eleanor K. Kolchin, Majorie M. Kohler, Yenking Wang, Barbara B. Baldwin y Robert J. Wisner, “Efecto sobre la energía de una mayor flexibilidad en el factor separable de Hylleraas -Type Atomic Wave Functions from H− to O VII”, Physical Review 112, 1187, 15 de noviembre de 1958.
- Verde, Louis C.; Matsushima, Satoshi; Kolchin, Eleanor K., “Tablas de las funciones de onda continuas para el hidrógeno”, Suplemento de revista astrofísica, vol. 3, noviembre de 1958, p.459.
- Green, Louis C., Cynthia Stephens, Eleanor K. Kolchin, et al., “He I Función de onda del estado fundamental de la forma ψ=f(r1)f(r2)g(r12)”, Journal of Chemical Physics 30 , 1061 (1959).
- Green, Louis C., Eleanor K. Kolchin, Norma C. Johnson, “Funciones de onda para los estados excitados del helio neutro”, Physical Review 139(2A):363-378, julio de 1965.
- Green, Louis C., Eleanor K. Kolchin, “Superficies de densidad equivalente en binarios cerrados de rotación síncrona construidos sobre el modelo politrópico ν = 3”, Astrofísica y ciencia espacial, número 2, abril de 1973, págs. 285-288.
Enlaces (actualizado el 31 de julio de 2017) :
- The Face Of A ‘Computer’ from 1946 , Huffington Post, entrevista de Eleanor Kolchin por Bianca Bosker, 25 de febrero de 2013 [ texto del artículo archivado localmente ].
- ” El memorando interno que permitió a las empleadas de IBM casarse “, The Atlantic , 4 de febrero de 2013 [ texto del artículo archivado localmente ].
- Comité de Mujeres de la Asociación para la Maquinaria de Computación, Premio Pionero del Centro Nacional para la Mujer y la Tecnología de la Información 2014 (Facebook, 21 de mayo de 2014, la misma imagen que arriba con la leyenda: “Eleanor Kolchin, ganadora del Premio Pionero NCWIT 2014. ¡Ella era una computadora! A los 88, la única persona en la habitación (sospecho) que realmente programó con clavijero”).
- Premio NCWIT Eleanor Kolchin Pioneer de 2014 (video del discurso de Krawitz-Kolchin).
- Eleanor Kolchin Profile, NCWIT Boca West Special Interest Club (2014) [ texto del artículo archivado localmente ].